1、本网站所提供的信息，只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内，本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时，必须以善意且谨慎的态度行事；访问者不得故意或者过失的损害本网站的各类合法权益，不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果，本网站不承担任何责任
5、本网站图片，文字之类版权，本网站无法鉴别所上传图片或文字的知识版权，如果侵犯，请及时通知我们，本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者，视为自愿接受本网站声明的约束。
试卷云
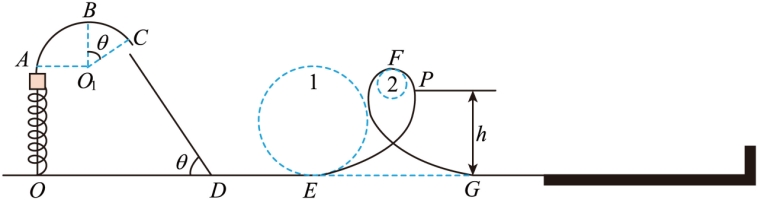
如图所示，一弹射装置由轨道OABC、直轨道CD和DE、左右对称的“雨滴”形曲线轨道EFG（F为最高点）和L形滑板组成。已知OA竖直，ABC是圆心在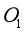
、半径
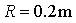的圆弧（B为最高点）。L形滑板质量
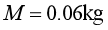，上表面（除突出部分）长为
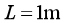，上表面的动摩擦因数
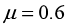，下表面光滑，其余轨道也均光滑。除L形滑板外，其余轨道均固定在地面上。弹簧下端固定，处于原长时上端与A和
都等高。B点距地面高度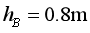
。
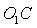与竖直方向夹角为
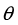，CD与水平方向夹角也为
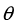，且
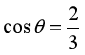。一质量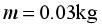
的小滑块穿套在轨道OABC上，不与弹簧相连，压缩弹簧后滑块被弹出，滑到C点飞出后，立刻沿CD下滑，CD与DE平滑相接。图中圆1和圆2分别为E、F两点的曲率圆，半径分别为
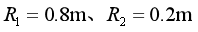，曲率圆的半径也称为曲线在该处的曲率半径。g取
。
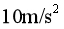(1)若已知弹簧劲度系数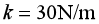
，则当小滑块放在弹簧上处于静止状态时，求弹簧的压缩量x；
(2)某次弹射后，发现滑块到达C点时恰好对轨道无作用力，求滑块运动到A处时的速度大小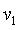
；
(3)某次弹射后，发现滑块在轨道EFG内运动时，其向心加速度大小恒为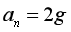
，求轨道EFG内任意高度h处的曲率半径
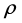与h的函数关系式。（提示：任意曲线运动的向心加速度
）
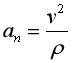(4)已知EFG轨道的形状及大小就是（2）问中所求的结果，滑块与L形滑板发生的碰撞是弹性碰撞。现要使滑块能到达、且不会从L形滑板上脱落，求滑块运动在A点时速度大小的取值范围。
【答案】(1)0.01m
(2)2m/s
(3)
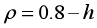
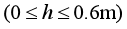
(4)
【知识点】利用动量守恒及能量守恒解决（类）碰撞问题、应用动能定理解多段过程问题、杆球类模型及其临界条件、胡克定律及其应用
【详解】（1）根据胡克定律
而
联立可得弹簧的压缩量为
（2）在C点，由牛顿第二定律
代入数据得
从A点到C点，由动能定理
代入数据得
（3）在E点
代入数据得
从E点到P点，由动能定理
解得
在P点
由以上式子解得
在F点
，
所以轨道EFG内任意高度h处的曲率半径
与h的函数关系式为
（4）①若滑块恰好过B点，即
由动能定理
解得
所以滑块若能过B点，则一定能过F点。由动能定理
可得滑块在A点时的速度最小值为
②滑块与L形滑板，由动量守恒定律
解得
且满足能量守恒定律
，
从A点到G点，由动能定理
解得
所以滑块运动在A点时速度大小的取值范围为
